| 18 Dec 02 |  | RCW 38 | This Chandra image revealed a diffuse cloud of X-rays enveloping the star cluster. |
| 18 Dec 02 |  | NGC 1700 | NGC 1700 may be the result of a merger of two smaller galaxies. |
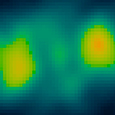
| 11 Dec 02 |  | SS 433 | This image shows two high speed lobes 5 trillion kilometers apart on opposite sides of a binary black hole system. |
| 19 Nov 02 |  | NGC 6240 | An extremely luminous galaxy about 400 million light years from Earth. |
| 07 Nov 02 |  | Mars | This remarkable image gave scientists their first look at X-rays from Mars. |
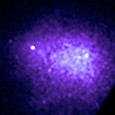
| 22 Oct 02 |  | NGC 720 | An elliptical galaxy located about 80 million light years from Earth in the Constellation Cetus. |
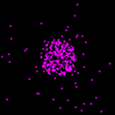
| 03 Oct 02 |  | XTE J1550-564 | A binary star system of a black hole and a normal star located in the Milky Way about 17,000 light years away. |
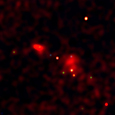
| 19 Sep 02 |  | Crab Nebula | The remnant of a supernova located 6000 light years from Earth in the constellation Taurus. |
| 13 Sep 02 |  | Abell 2104 | A galaxy cluster in the constellation Serpens. |
| 06 Sep 02 |  | Tycho's Supernova Remnant | The remains of a supernova about 7,500 light years from Earth. |
| 19 Aug 02 |  | Cassiopeia A | 320 year old remnant of a massive star that exploded in the constellation Cassiopeia. |
| 07 Aug 02 |  | Centaurus A Arcs | An active galaxy located about 11 million light years from Earth in the constellation Centaurus. |
| 31 Jul 02 |  | Hot Intergalactic Gas
(PKS 2155-304) | This artist's conception depicts a huge cloud of hot gas 800 million light years from Earth. |
| 23 Jul 02 |  | NGC 1569 | A dwarf galaxy approximately 7 million light years from Earth. |
| 02 Jul 02 |  | Whirlpool Galaxy
(M51) | A pair of galaxies about 30 million light years from Earth. |
| 28 Jun 02 |  | NGC 3516 | Scientists Observe Light Fighting To Escape Black Hole's Pull |
| 25 Jun 02 |  | SNR G54.1+0.3 | A distant supernova remnant with a bright ring of high-energy particles and a central point-like source. |
| 06 Jun 02 |  | 1E 1207.4-5209 | This artist's conception depicts a neutron star located about 7,000 light years from Earth. |
| 04 Jun 02 |  | NGC 4649 | The elliptical galaxy NGC 4649 reveals diffuse hot gas dotted with many point-like sources. |
| 04 Jun 02 |  | NGC 1553 | The elliptical galaxy NGC 1553 reveals diffuse hot gas dotted with many point-like sources. |
| 04 Jun 02 |  | NGC 4697 | The elliptical galaxy NGC 4697 reveals diffuse hot gas dotted with many point-like sources. |
| 22 May 02 |  | N132D | A supernova remnant located in the Large Magellanic Cloud about 160,000 light years from Earth. |
| 07 May 02 |  | Arp 270 | Arp 270 shows two galaxies about 90 million light years from Earth in the early stage of a merger. |
| 23 Apr 02 |  | Tarantula Nebula
(30 Doradus) | Tarantula Nebula gives scientists a close-up view of the drama of star formation and evolution. |
| 19 Apr 02 |  | Arp 220 | Arp 220 gives new insight into what happens when two galaxies the size of the Milky Way collide. |
| 10 Apr 02 |  | RX J1856.5-3754 | A compact star about 400 light years from Earth in the constellation Corona Australis. |
| 10 Apr 02 |  | 3C58 | A supernova remnant with a central pulsar about 10,000 light years from Earth in the constellation Cassiopeia. |
| 04 Apr 02 |  | Coma Cluster | A cluster of galaxies about 500 million light years from Earth in the constellation Coma Berenices. |
| 28 Mar 02 |  | SDSS 0836+0054 | A quasar 13 billion light years from Earth. |
| 28 Mar 02 |  | SDSS 1030+0524 | A quasar 13 billion light years from Earth. |
| 28 Mar 02 |  | SDSS 1306+0356 | A quasar 13 billion light years from Earth. |
| 13 Mar 02 |  | Quasar Pair Q2345+007 A, B | A closely aligned pair of quasars about 11 billion light years from Earth in the constellation Pisces. |
| 27 Feb 02 |  | Jupiter | The fifth planet away from the Sun, it is the largest planet in our solar system. |
| 20 Feb 02 |  | 1E 0657-56 | An extremely hot galaxy cluster about 4 billion light years from Earth. |
| 06 Feb 02 |  | PKS 1127-145 | A quasar about 10 billion light years from Earth located in the constellation Crater. |
| 29 Jan 02 |  | Centaurus Cluster | A cluster of galaxies about 170 million light years from Earth, located in the constellation Centaurus. |
| 09 Jan 02 |  | Galactic Center Survey | A 400 by 900 light-year mosaic of images located about 25,000 light years from Earth. |
| 09 Jan 02 |  | Galactic Center Radio Arc | Observations of a region of the Galactic Center found an X-ray filament and cloud. |
| 08 Jan 02 |  | Abell 2597 | A cluster of galaxies about a billion light years from Earth, located in the constellation Aquarius. |
