September 22, 2005
CXC RELEASE: 05-07
Astronomers have found compelling evidence that a supernova shock wave has produced a large amount of cosmic rays, particles of mysterious origin that constantly bombard the Earth. This discovery, made with NASA's Chandra X-ray Observatory, supports theoretical arguments that shock waves from stellar explosions may be a primary source of cosmic rays.
This finding is important for understanding the origin of cosmic rays, which are atomic nuclei that strike the Earth's atmosphere with very high energies. Scientists believe that some are produced by flares on the Sun, and others by similar events on other stars, or pulsars or black hole accretion disks. But, one of the prime suspects has been supernova shock waves. Now, a team of astronomers has used Chandra observations of Tycho's supernova remnant to strengthen the case for this explanation.
"With only a single object involved we can't state with confidence that supernova shock waves are the primary source of cosmic rays," said John P. Hughes of Rutgers University in Piscataway, New Jersey, and coauthor of a report to be published in an upcoming issue of The Astrophysical Journal. "What we have done is present solid evidence that the shock wave in at least one supernova remnant has accelerated nuclei to cosmic ray energies."
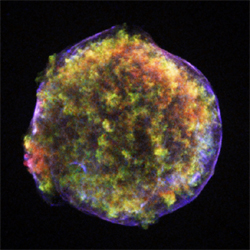
In the year 1572, the Danish astronomer Tycho Brahe observed and studied the sudden appearance of a bright "new star" in the constellation Cassiopeia. Now known as Tycho's supernova remnant, the event created a sensation in Tycho's time because it exploded the myth that stars never change.
Four centuries later, the Chandra results on Tycho's remnant show that some modern ideas of the aftermath of supernova explosions may have to be revised. The report by Hughes and colleagues demonstrates that the shock wave produced by the explosive disruption of the star behaves in a way that cannot be explained by the standard theory.
The supernova debris is observed to expand at a speed of about six million miles per hour. This rapid expansion has created two X-ray emitting shock waves - one moving outward into the interstellar gas, and another moving inward into the stellar debris. These shock waves, analogous to the sonic boom produced by supersonic motion of an airplanes, produce sudden, large changes in pressure, and temperature behind the wave.
According to the standard theory, the outward-moving shock should be about two light-years ahead of the stellar debris (that's half the distance from our sun to the nearest star). What Chandra found instead is that the stellar debris has kept pace with the outer shock and is only about half a light-year behind.
"The most likely explanation for this behavior is that a large fraction of the energy of the outward-moving shock wave is going into the acceleration of atomic nuclei to speeds approaching the speed of light," said Jessica Warren, also of Rutgers University, and the lead author of the report in the Astrophysical Journal.
Previous observations with radio and X-ray telescopes had established that the shock wave in Tycho's remnant was accelerating electrons to high energies. However, since high-speed atomic nuclei produce very weak radio and X-ray emission also, it was not known whether the shock wave was accelerating nuclei as well. The Chandra observations provide the strongest evidence yet that nuclei are indeed accelerated, and that the energy contained in high-speed nuclei is about 100 times that in the electrons.
Hughes also pointed out that the Chandra result for Tycho's remnant significantly changes astronomers' view of the evolution of supernova remnants. A large component of cosmic ray nuclei alters the dynamics of the shock wave, and may require changing the way that astronomers estimate the explosive energy of a supernova from the properties of its remnant.
NASA's Marshall Space Flight Center, Huntsville, Ala., manages the Chandra program for the agency's Science Mission Directorate. The Smithsonian Astrophysical Observatory controls science and flight operations from the Chandra X-ray Center in Cambridge, Mass.
Additional information and images are available at:
MEDIA CONTACTS
Joseph Blumberg
Rutgers University
(Phone: 732-932-8412 ext. 652)
Steve Roy
Marshall Space Flight Center, Huntsville, Ala.
(Phone: 256/544-6535)
Megan Watzke
Chandra X-ray Center, Cambridge, Mass.
(Phone: 617/496-7998)